Inter-intra cellular pilot contamination mitigation for heterogeneous massive MIMO cellular systems

Abstract

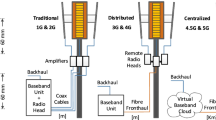
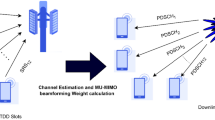
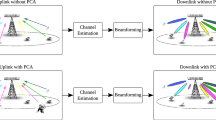
Massive multiple-input-multiple-output (MIMO) technology has been advocated as one of the most advanced and promising technologies for catering to the high data requirements of present and future cellular networks. It can be achieved by the installation of hundreds or thousands of antennas at the base station (BS), for serving tens of users. For making proper use of its high gain capabilities, it is required for the BS to have full knowledge of the channel between the users and itself which is obtained using channel state information (CSI). Pilot contamination has been identified as a major hindrance in the error-free computation of CSI. In this paper, a heterogeneous massive MIMO cellular system has been considered where the number of users present in different cells are assumed to be different. Moreover, the same pilots are reused by the users of each cell. This gives rise to the scenario of both inter-cellular and intra-cellular pilot contamination in the massive MIMO cellular system approach. To mitigate these aforesaid pilot contamination, two sub-optimal algorithms have been proposed in this correspondence which allocate the available same pilots to various users in a systematic manner based upon their perceived interference. In the first approach, the intra-cellular pilot contamination has been addressed before addressing the inter-cellular pilot contamination. The inter-cellular pilot contamination has been resolved ahead of the intra-cellular pilot contamination as per the second approach. Both these algorithms are designed with the aim of maximizing the system throughput. Hence, pilots with low interference are allocated to better channel conditioned users and vice-versa. On different performance parameters, the algorithms are evaluated and the simulation results show that the second pilot allocation strategy is more successful than the first scheme incurring the same computational complexity. Moreover, the effectiveness of the proposed algorithms have been presented by comparing with existing pilot contamination mitigation algorithms for various system metrics.

Computational complexity analysis

1.1 Computational complexity analysis of the proposed algorithms

Considering the first algorithm, the complexity of finding the cell index having minimum user $K_{min}$ is given by,

$$\begin{aligned} V_1 = O(L). \end{aligned}$$

(A1)

Iterations for finding the best user in the target cell along with its highest matched antenna along with BS antenna and alloting it a pilot is,

$$\begin{aligned} V_2 = MK_{min}N. \end{aligned}$$

(A2)

Thus, total iterations required for alloting all the P pilots in the target cell,

$$\begin{aligned} V_3&=PMK_{min}N \nonumber \\&=MK_{min}^2N, \text { since } P = K_{min}. \end{aligned}$$

(A3)

Similaly, the total iterations required for alloting the P pilots to all the users present in the other cells (except the target cell) is,

$$\begin{aligned} V_4&=(L-1)PMK_{l}N\dfrac{K_l}{P}, \nonumber \\&=(L-1)MK_{l}^2N, \end{aligned}$$

(A4)

where $\dfrac{K_l}{P}$ denotes the number of reuses in that cell. Hence, total iterations required for allocating pilots to all the users,

$$\begin{aligned} V_5&=V_4+V_3 \nonumber \\&=(L-1)MK_{l}^2N+MK_{min}^2N \nonumber \\&\approxeq LMK_{total}^2N. \end{aligned}$$

(A5)

Finally, the total computational complexity of the entire process,

$$\begin{aligned} T&=V_1+V_5 \nonumber \\&=O(L)+O(LMK_{total}^2N) \nonumber \\&\approxeq O(LMK_{total}^2N), \text { since } LMK_{total}^2N>> L. \end{aligned}$$

(A6)

Both the proposed algorithms have the same computational complexity.

1.2 Computational complexity analysis of the ESA

The complexity of finding the cell index having minimum user among all cells, $K_{min}$ is given by,

$$\begin{aligned} V_1 = O(L). \end{aligned}$$

(A7)

Total number of combinations that can be formed with user number, user antenna number and BS antenna number is given by,

$$\begin{aligned} X = MK_{min}N. \end{aligned}$$

(A8)

For each combination in the above expression, the number of combinations in the next randomly chosen cell with K$_{l}$ users is given by,

$$\begin{aligned} X_{l} = MK_{l}N. \end{aligned}$$

(A9)

Thus, for total number of combinations to be checked to reach the optimal solution, is given by,

$$\begin{aligned} J&= \prod _{i=1}^{L} X_{l}, \nonumber \\&= MK_{1}N \times MK_{2}N \times \ldots \times MK_{L}N, \nonumber \\&= (MK_{min}N)^L\prod _{i=1}^{L} R_{l}, \end{aligned}$$

(A10)

where $R_{l}$ is the reuse factor of $l_{th}$ cell. Thus the total computational complexity of ESA is given by,

$$\begin{aligned} C&= O(J) + V_1 \nonumber \\&\approxeq O(J) = O((MK_{min}N)^L\prod _{i=1}^{L} R_{l}) \end{aligned}$$

(A11)

1.3 Computational complexity analysis of the OPA [30]

From [30], we know that the complexity of the OPA strategy is given as $O\left( K_{active}log(K_{active})\right)$, where K$_{active}$ is the number of users present within the considered area. When we implement the algorithm for our system model, number of BS antennas as well as user antennas come into account, which alters the complexity slightly. The updated complexity of the OPA scheme can then be given as $O\left( K_{active}MNlog(K_{active}MN)\right)$.

1.4 Computational complexity analysis of the JPO [31]

From [31], we know that the complexity of the JPO strategy is given as $O\left( K\chi _p^3+K\chi _pM\right)$, where K is the number of users. When we implement the algorithm in our system model, number of user antennas also come into account, which alters the complexity slightly. The updated complexity of the JPO scheme can then be given as $O\left( K_{total}\chi _p^3+K_{total}\chi _pMN\right)$.

1.5 Computational complexity analysis of the RA scheme

Choosing a target cell l, the number of ways in which any random user may be selected from all users for assigning the first pilot is,

$$\begin{aligned} C_l=M \times N \end{aligned}$$

(A12)

For all the K$_{l}$ users in the l$_{th}$ cell, number of iterations required is,

$$\begin{aligned} C_2=K_l \times M \times N \end{aligned}$$

(A13)

Hence for all the cells, the number of iterations required is,

$$\begin{aligned} C_3=M \times N \times L \times \sum _{l=1}^L K_l = MNLK_{total}, \end{aligned}$$

(A14)

where $K_{total} = \sum _{l=1}^L K_l$. Thus, the computational complexity of RA strategy is of the order of $O\left( MNLK_{total}\right)$.